Назад

Олимпиадная задача: Кентавр на квадратной доске 1000×1000 — теория алгоритмов

Задача 209542 • Сложность: 3 • 7-9 класс
Задача

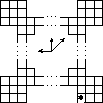
Из квадратной доски 1000×1000 клеток удалены четыре прямоугольника 2×994 (см. рис.).

На клетке, помеченной звездочкой, стоиткентавр– фигура, которая за один ход может перемещаться на одну клетку вверх, влево или по диагонали вправо и вверх. Двое игроков ходят кентавром по очереди. Проигрывает тот, кто не может сделать очередной ход. Кто выигрывает при правильной игре?

Авторы:
Женодаров Р. Г.
Разделы:
Текстовые задачи Теория алгоритмов
Источники:
Олимпиады и турниры Всероссийская олимпиада по математике 1992-1993 Региональный этап
Количество версий:
4
Решение

  Заметим, что игра не может продолжаться бесконечно: ходов каждого типа можно сделать не более 999. Рассмотрим правый нижний фрагмент доски квадрат 3×3 (см. рис.). Пусть кентавр оказался в клетке a3. Игрок, делающий ход с a3, либо выигрывает, либо проигрывает.

  В первом случае второй игрок может добиться того, чтобы делать ход с этой клетки  (a1 → a2 → b3 → a3  или  a1 → b2 → b3 → a3),  а во втором случае он может заставить своего противника ходить с a3  (a1 → a2 → a3  или  a1 → b2 → c3 → b3 → a3).  Поэтому при правильной игре второй игрок выигрывает.

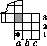
Ответ

Второй игрок.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет