Олимпиадная задача Токарева: стрелки на сторонах и диагоналях правильного 2n-угольника

Решение 1:   Будем называть диагональ правильного многоугольника главной, если она проходит через его центр. Для каждой неглавной диагонали существует симметричная ей относительно центра неглавная диагональ. Таким образом, все неглавные диагонали разбиваются на пары. Поставив в каждой такой паре стрелки в противоположных направлениях, мы получим векторы, дающие в сумме 0 (рис. слева).

  Осталось расставить стрелки на сторонах и главных диагоналях. В случае  n= 2k+ 1  сначала расставим стрелки по циклу A₁A_n+1A_n+2A₂A₃A_n+3A_n+4...A_2n–2A_2n–1A_n–1A_nA_2nA₁, полученные векторы в сумме дадут0(рис. справа).   В случае  n= 2k  выделим в многоугольнике циклы, состоящие из пар соседних главных диагоналей и соединяющих их сторон. В каждом цикле поставим стрелки так, чтобы сумма получившихся векторов была равна0.   В обоих случаях осталось поставить стрелки на сторонах, взятых через одну. Расставим их по циклу и получим0, так как каждый вектор переходит в следующий при повороте на угол^2π/_nвокруг центра.

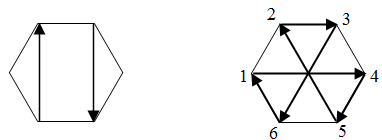
Решение 2:   Взяв вершины 2n-угольника  (n ≥ 3)  через одну, получим два правильных n-угольника M₁ и M₂. Предположим, что мы умеем решать задачу для правильного n-угольника. Для того чтобы решить её для 2n-угольника, достаточно расставить стрелки на сторонах и диагоналях каждого из многоугольников M₁ и M₂, а потом из каждой вершины M₁ провести векторы во все вершины M₂. Последняя система векторов переходит в себя при повороте на угол ^2π/_n вокруг центра, следовательно, её сумма равна 0 (рис. слева).

  Еслиnнечётно, проведём из каждой вершины векторы в следующие за ней  ^n–1/₂  вершин. Их сумма равна0, так как она не изменится при повороте на угол^2π/_nвокруг центра (рис. справа).   Итак, мы можем, начав с квадрата (для него утверждение очевидно) или нечётноугольника, удвоением числа сторон получить требуемую расстановку стрелок для любого правильного 2n-угольника.

Ответ задачи отсутствует