Олимпиадная задача по стереометрии о пирамидах и сферах (10-11 класс, Соловьев И.)
Задача
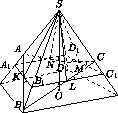
Точка O – основание высоты четырёхугольной пирамиды. Сфера с центром O касается всех боковых граней пирамиды. Точки A, B, C и D взяты последовательно по одной на боковых ребрах пирамиды так, что отрезки AB, BC и CD проходят через три точки касания сферы с гранями.
Докажите, что отрезок AD проходит через четвёртую точку касания.
Решение
Пусть S – вершина пирамиды, K, L, M и N – точки касания сферы с гранями пирамиды (см. рис.). Отрезки SK, SL, SM и SN равны как отрезки касательных, проведённых к сфере из точки S. Значит, точки K, L, M и N лежат ещё и на сфере с центром в точке S и радиусом SK, а следовательно, и на одной окружности, являющейся линией пересечения этой сферы с данной. Плоскость этой окружности перпендикулярна линии центров SO сфер, то есть параллельна плоскости основания пирамиды, а поэтому пересекает её боковые ребра. Обозначим эти точки пересечения через A1, B1, C1 и D1. Соединим точку N с точками A и D. Треугольники AA1N и AA1K равны, так как A1K = A1N, AK = AN (отрезки касательных, проведённых к сфере из одной точки), а сторона AA1 у них общая. Следовательно, ∠ANA1 = ∠AKA1. Аналогично ∠BKB1 = ∠BLB1, ∠CLC1 = ∠CMC1 и ∠DMD1 = ∠DND1. Кроме того,
∠AKA1 = ∠BKB1, ∠BLB1 = ∠CLC1 и CMC1 = ∠DMD1 как вертикальные. Поэтому ∠ANA1 = ∠DND1, следовательно, точка N лежит на отрезке AD.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь