Олимпиадная задача по планиметрии: точки пересечения лучей и окружностей, Купцов Л.

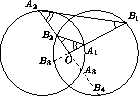
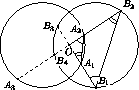
Пусть A₁ и A₂ – точки, лежащие на первой окружности, а B₁ и B₂ – точки, лежащие на второй окружности. Обратимся к ситуации, изображенной на 1021 (случай, изображенный на 1022 рассматривается аналогично).

Пусть точки A₃ , B₃ и B₄ симметричны точкам B₂ , A₁ и A₂ соответственно относительно точки O . По теореме о пересекающихся хордах B₃O· OB₁=B₂O· OB₄ , откуда OA₁· OB₁=OB₂· OA₂ , так как B₃O=OA₁ и OB₄=OA₂ . Это и означает, что точки A₁ , B₁ , B₂ и A₂ лежат на одной окружности.

В случае, показанном на 1021,B₂B₃=A₁A₃ в силу симметрии этих дуг относительно точки O . Поэтому A₃A₂A₁= B₃B₁B₂ , т.е. отрезок A₁B₂ виден из точек B₁ и A₂ под одинаковым углом, следовательно, точки A₁ , A₂ , B₁ и B₂ лежат на одной окружности.

В случае, изображенном на 1022,B₂B₃=A₁A₃ , A₃A₂A₁= B₃B₁B₂ , но A₁A₂B₂=180^o- A₃A₂A₁ , поэтому B₃B₁B₂+ A₁A₂B₂=180^o .

Ответ задачи отсутствует