Олимпиадная задача по планиметрии: медианы прямоугольных треугольников и их углы

Параллельным переносом одного из двух данных треугольников совместим вершины C и C' их прямых углов, а гомотетией того же треугольника с центром в точке C совместим их медианы 112. 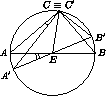Тогда окружность с центром E и радиусом CE описана около обоих треугольников, причем угол между их гипотенузами – центральный и, значит, вдвое больше соответствующего вписанного угла, каковым является один из углов между катетами (на 112 это углы: AEA'=2 ACA' ). Для доказательства требуемого утверждения остается заметить, что проделанные выше преобразования одного из треугольников не меняют углов между прямыми.

Ответ задачи отсутствует