Олимпиадная задача по планиметрии: определение периметра многоугольника в круге 10–11 класс

а) Первое решение. Пусть Коля указал три прямые l₁ , l₂ и l₃ . Без ограничения общности далее считаем, что эти прямые различны и каждая из них имеет с данным кругом хотя бы одну общую точку. Покажем, что найдутся два многоугольника, удовлетворяющие условиям задачи и пересекающие каждую из этих прямых, периметры которых отличаются более чем на0,6.

Пусть A и B – середины двух дуг, высекаемых прямой l₁ на данной окружности ( AB – диаметр данного круга). Пусть также C и D – отличные от A и B точки пересечения данной окружности с прямыми l₂ и l₃ соответственно. Многоугольник с вершинами A , B , C и D удовлетворяет условию задачи и пересекает каждую из прямых l₁ , l₂ и l₃ . Его периметр P₁ не превосходит суммы длин отрезков AC , CB , AD и DB , а значит, и периметра вписанного в данный круг квадрата, т.е. P₁ 4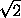<4· 1,42=5,68. Добавляя к этому многоугольнику вершины на данной окружности, можно добиться того, что его периметр P₂ станет близок к2π , именно, P₂>2·3,14=6,28. Коля не сможет "отличить" два указанных многоугольника, а значит, не сможет и наверняка угадать периметр с точностью до0,3<(P₂-P₁)/2. Второе решение. Предположим, что Коле удалось придумать способ наверняка угадать за3хода периметр многоугольника с точностью до0,3. Для каждой из трех указанных Колей прямых Миша отвечает, пересекает ли эта прямая загаданный многоугольник. По предположению для каждого из8возможных наборов таких ответов Коля придуманным им способом определяет значение периметра с точностью до0,3. Следовательно, настоящее значение периметра может принадлежать одному из8числовых отрезков суммарной длины не более8· 0,6= 4,8. С другой стороны, периметр многоугольника из условия задачи может принимать любое значение из интервала(0,2π)длины2π>4,8. Следовательно, среди них найдется такой многоугольник, угадать периметр которого с требуемой точностью Коле не удастся. Приходим к противоречию. б) Построим систему координат Oxy с началом координат в центре O данного круга. Пусть q – натуральное число. Для любого k=0,1,..,q-1обозначим через Ox_k ось, повернутую против часовой стрелки вокруг точки O на угол ϕ_k:= π kq ( Ox₀ Ox ). Для любого натурального p при каждом фиксированном k=0,1, .., q-1мы сможем найти приближенное значениеd_k длины d_k ортогональной проекции[a_k,b_k]( a_k 0 b_k ) загаданного многоугольника на ось Ox_k с точностью до1/2^p . Для этого будем последовательно указывать прямые l_k,m ( m=1,2,..,p ), перпендикулярные оси Ox_k и пересекающие ее в точках с координатами r_m/2^m . Положим r₁=1и r_m+1=2r_m+1, если прямая l_k,m пересекла загаданный многоугольник, и r_m+1=2r_m-1в противном случае. Тогда величина r_p+1/2^p+1равна b_k с точностью до1/2^p+1. Аналогично, за оставшиеся p попыток определим с той же точностью величину a_k .

Покажем, что величина2 sin · _k=0^q-1d_k при правильном выборе p и q определяет с требуемой точностью периметр P загаданного многоугольника. Пусть N – количество его сторон. Обозначим их Δ_j ( j=1,2,..,N ), через |Δ_j| обозначим их длины, а через D_j,k – длины их ортогональных проекций на ось Ox_k . Каждая точка интервала(a_k,b_k)является ортогональной проекцией ровно двух точек границы загаданного многоугольника. Значит, _j=1^N D_j,k =2d_k . Положим где- величины углов между сторонойи осью Ox_k(k=0,1,..,q-1; считаем знак величины угла положительным, если кратчайший поворот, переводящий сторонув параллельный оси Ox_kотрезок, происходит против часовой стрелки, и отрицательным в противном случае), а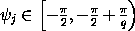- меньшая из этих величин. Имеем Так как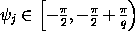, мы получаем, чтои Отсюда и из неравенства P<2π следует, что 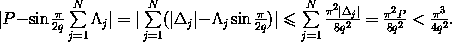Значит, 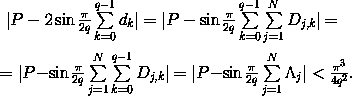Отсюда получаем Полагая p=11и q=90, получаем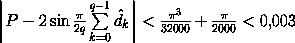(так как π<<3,2). При этом для определения величинd_k мы потратили2p· q =1980 < 2007попыток. Комментарий. Предложенный в решении способ приближенного нахождения периметра выпуклого многоугольника с помощью длин его ортогональных проекций на различные прямые приводит нас к важной формуле современного анализа. Формула Фавара

позволяет находить точные значения периметра P произвольной выпуклой фигуры с помощью интеграла от длины l(ϕ)ее ортогональной проекции на прямую, образующую угол ϕ с осью Ox .

Например, эта формула позволяет нам установить интересный факт, что всякая выпуклая фигура, длина ортогональной проекции которой на любую прямую равна d (такие фигуры называются фигурами постоянной ширины), имеет тот же периметр, что и круг такого диаметра. [1] Фавар (Favard J.). Definition de la longueur et de l'aire. – C. R. Acad. Sci. Paris. 1932. V.194. P.344-346. [2] Гарднер М. Математические досуги, гл. 23. Кривые постоянной ширины. – М.: "Мир", 2000.

а) нет; б) да.