Задачи Подборки Авторы

Олимпиадная задача по планиметрии: равенство медиан в треугольниках ADB и CDB

Задача 209466 • Сложность: 2 • 8-9 класс

Задача

На стороне AC треугольника ABC взята точка D так, что AD:DC=1:2. Докажите, что у треугольников ADB и CDB есть по равной медиане.

Решение

Пусть K и M – середины BD и BC соответственно (см. рис. 8.5). Тогда по теореме о средней линии треугольника KM||DC и KM=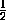DC , то есть KM||AD и KM=AD . Это означает, что AKMD – параллелограмм, а тогда AK=DM . Это и есть искомые равные медианы.