Олимпиадная задача: три квадратных трёхчлена и их графики – многочлены и доказательство
Задача
На рисунке изображены графики трёх квадратных трёчленов.
Можно ли подобрать такие числа a, b и c, чтобы это были графики трёхчленов ax² + bx + c, bx² + cx + a и cx² + ax + b?
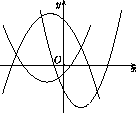
Решение
Решение 1:Пусть это удалось. У двух парабол "ветви" направлены вверх, а у одной – вниз, поэтому у двух трёхчленов старший коэффициент положительный, а у одного – отрицательный. Следовательно, среди чисел a, b и c должны быть два положительных и одно отрицательное. С другой стороны, две из парабол пересекают ось Оy в точках с отрицательными ординатами, а третья – в точке с положительной ординатой, поэтому у двух трёхчленов свободный член отрицательный, а у одного – положительный. Следовательно, среди чисел a, b и c должны быть два отрицательных и одно положительное. Противоречие.
Решение 2: Такие параболы имеют общую точку (1, a + b + c). Но на рисунке такой точки нет.
Ответ
Нельзя.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь