Олимпиадная задача по тригонометрии для 9–11 классов: доказательство существования решений
Задача
Доказать, что каковы бы ни были числа a, b, c, по крайней мере одно из уравнений
a sin x + b cos x + c = 0, 2a tg x + b ctg x + 2c = 0
имеет решение.
Решение
Преобразуем первое уравнение, введя вспомогательный угол:
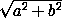sin(x + ϕ) + c = 0. Это уравнение не имеет решений, если |c| > 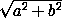, то есть если c² > a² + b².
Второе уравнение заменой t = tg x сводится к квадратному 2at² + 2ct + b = 0, которое не имеет решений, если c² – 2ab < 0. (Корень t = 0 может оказаться посторонним, но он является единственным корнем только при b = c = 0, а в этом случае первое уравнение имеет решение.) Но в силу неравенства Коши условия c² > a² + b² и c² < 2ab не могут выполняться одновременно.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь