Олимпиадная задача по планиметрии для 8–9 класса: шестиугольник и описанная окружность

Первое решение:

Пусть в шестиугольнике ABCDEK; AB||DE, BC||EK, CD||KA, AD=BE=CK . Из условия задачи следует, что четырехугольники ABDE, BCEK, CDKA являются трапециями, причем равнобедренными, так как их диагонали равны (рис.). Поэтому они будут иметь оси симметрии, представляющие собой срединные перпендикуляры к параллельным сторонам трапеций. Эти оси – биссектрисы углов между диагоналями, а вместе с тем биссектрисы углов треугольника NLM , образованного точками пересечения диагоналей трапеций. Следовательно, эти три оси пересекутся в одной точке O , которая и будет центром окружности, описанной вокруг данного шестиугольника, так как лежит на срединных перпендикулярах всех сторон шестиугольника.

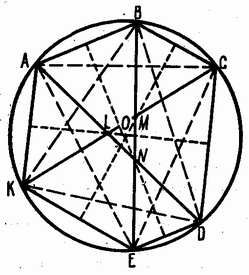
Второе решение:

Пусть ABCDEF — шестиугольник, удовлетворяющий условию задачи. Четырёхугольник FBCE является равнобочной трапецией, поэтому прямая MM₁, соединяющая середины её оснований, перпендикулярна к ним и служит биссектрисой угла между диагоналями BE и FC. Точно так же доказываются аналогичные свойства прямых NN₁ и LL₁, соединяющих середины противоположных сторон шестиугольника. Эти три прямые являются биссектрисами углов треугольника, образованного диагоналями, поэтому они пересекаются в одной точке O. Точка O равноудалена от всех вершин шестиугольника, поскольку она лежит на всех серединных перпендикулярах к сторонам шестиугольника. Значит, вокруг шестиугольника можно описать окружность с центром O.

Ответ задачи отсутствует