Олимпиадная задача по алгебраическим неравенствам для 8-10 классов: доказательство неравенства для произведения четырёх чисел
Задача
Дано четыре положительных числа a, p, c, k, произведение которых равно 1. Доказать, что a² + p² + c² + k² + ap + ac + pc + ak + pk + ck ≥ 10.
Решение
Первый способ. Согласно неравенству Коши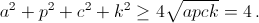 
По тому же неравенству 
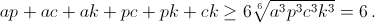Сложив почленно два полученных неравенства, получим требуемое. Второй способ. ap + ck = ap + 1/ap ≥ 2, аналогично, ac + ck ≥ 2, ak + pc ≥ 2. Кроме того, a² + p² + c² + k² ≥ 2(ap + ck) ≥ 4.
Осталось сложить все четыре неравенства.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет