Назад

Олимпиадная задача по планиметрии и алгебраическим методам: деление стороны треугольника (8-9 класс)

Задача 208681 • Сложность: 3 • 8-9 класс
Задача

Точки P1, P2, ..., Pn–1 делят сторону BC равностороннего треугольника ABC на n равных частей:  BP1 = P1P2 = ... = Pn–lC.  Точка M выбрана на стороне AC так, что  AM = BP1.

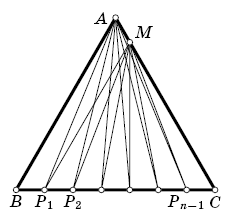
Докажите, что  ∠AP1M+ ∠AP2M+ ... + ∠APn–1M= 30°,  если   а)  n= 3;   б)n– произвольное натуральное число.
Решение

См. задачу 198309.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет