Олимпиадная задача по математике: периметр четырёхугольника и диагональ

Задача

В прямоугольник вписан четырёхугольник (на каждой стороне прямоугольника по одной вершине четырёхугольника).

Докажите, что периметр четырёхугольника не меньше удвоенной диагонали прямоугольника.

Решение

Трижды отразим прямоугольник ABCD с вписанным в него четырёхугольником KLMN (см. рис.).

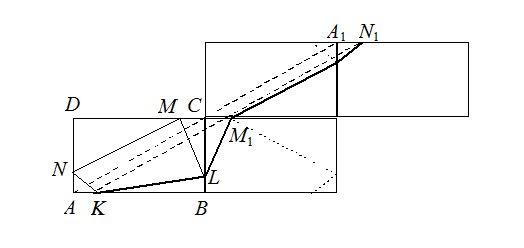
Легко видеть, что периметр четырёхугольника равен длине ломанойKLM₁N₁, которая не меньше длины отрезкаKN₁. Этот отрезок равен отрезкуAA₁, который вдвое больше диагоналиAC.

Ответ

Ответ задачи отсутствует

Олимпиадная задача по планиметрии: периметр четырёхугольника и диагональ прямоугольника

Задача

Решение

Ответ

Подтверждение удаления