Олимпиадная задача по планиметрии для 8-9 класса: совпадение точек в треугольнике
Задача
Треугольник ABC вписан в окружность. Точка A1 диаметрально противоположна точке A, точка A0 – середина стороны BC, точка A2 симметрична точке A1 относительно точки A0. Точки B2 и C2 определяются аналогично. Докажите, что точки A2, B2 и C2 совпадают.
Решение
Решение 1:Точки A2, B2 и C2 совпадают с ортоцентром H треугольника ABC – см. решение задачи 208949.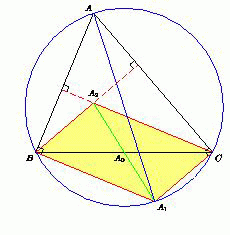 
Решение 2:Пусть O – центр окружности. Имеем: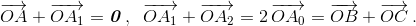 
Следовательно, 
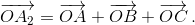То же верно для 
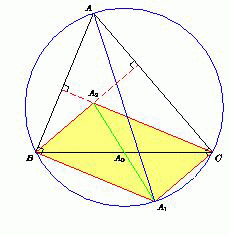и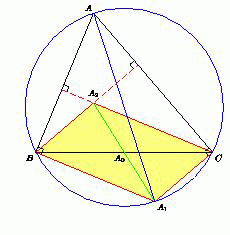 
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет