Олимпиадная задача по планиметрии: периметр шестиугольника и перемещения треугольников
Задача
Рассматривается шестиугольник, который является пересечением двух (не обязательно равных) правильных треугольников.
Докажите, что если параллельно перенести один из треугольников, то периметр пересечения (если оно остаётся шестиугольником), не меняется.
Решение
Рассмотрим объединение двух данных треугольников. Оно состоит из шестиугольника пересечения H и шести подобных между собой треугольников (см. рис.; один из углов каждого такого треугольника равен 60°, а два других – α и 120° – α). Если a – сторона такого треугольника, лежащая против угла в 60° (она также является стороной шестиугольника H), а Pa – периметр этого треугольника, то отношение k = a/Pa одно и то же для каждого из шести таких треугольников и не меняется при параллельном переносе. Периметр шестиугольника H равен сумме периметров шести подобных треугольников, умноженной на k. Осталось заметить, что сумма периметров шести подобных треугольников равна сумме периметров двух исходных правильных треугольников. 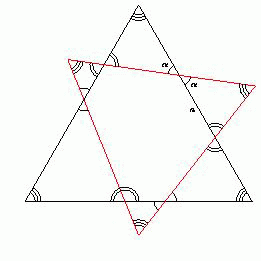
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь