Олимпиадная задача по планиметрии для 8–10 классов: параллелограммы внутри треугольника
Задача
Дан треугольник A0B0C0. На отрезке A0B0отмечены точки A1, A2, ,An , а на отрезке B0C0– точки C1, C2, , Cn , причём все отрезки AiCi+1( i=0,1, n-1), параллельны между собой и все отрезки CiAi+1( i=0,1, n-1) – тоже. Отрезки C0A1, A1C2, A2C1и C1A0ограничивают некоторый параллелограмм, отрезки C1A2, A2C3, A3C2и C2A1– тоже и т.д. Докажите, что сумма площадей всех n-1получившихся параллелограммов меньше половины площади треугольника A0B0C0.
Решение
Пусть D0– точка пересечения A0C1и C0A1, D1– точка пересечения A1C2и C1A2, D2– точка пересечения A2C3и C2A3и т.д.
Пусть прямая, проведённая через точку D1параллельно A0B0, пересекает A0C1в точке F , а прямая, проведённая через точку D1параллельно B0C0, пересекает C0A1в точке G . Тогда четырёхугольник A0A1D1F – параллелограмм, равновеликий параллелограмму D0A1D1C1, т.к. эти параллелограммы имеют общие основание A1D1и высоту, проведённую к этому основанию. Аналогично, равновелики параллелограммы C0GD1C1и D0A1D1C1. Значит,
SD0A1D1C1 =
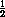(SA0A1D1F+SC0GD1C1) <
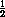SA0A1D1C1C0D0.
SD1A2D2C2 < 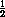SA1A2D2C2C1D1.
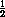(SΔ A0B0C0 - SA0D0C0) <
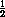SΔ A0B0C0,
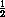
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь