Олимпиадная задача по планиметрии: точки пересечения касательных в равнобедренной трапеции
Задача
Дан угол с вершиной B. Возьмём произвольную равнобедренную трапецию, боковые стороны которой лежат на сторонах данного угла. Через две противоположные её вершины проведём касательные к описанной около неё окружности. Через M обозначим точку пересечения этих касательных. Какую фигуру образуют все такие точки M?
Решение
Пусть ADEC – равнобедренная трапеция, DM и CM – касательные к её описанной окружности (то есть M – некоторая точка искомого ГМТ), K – точка на продолжении отрезка DM за точку D. Тогда ∠BDM = ∠ADK = ∠ACD = ∠CAE = ∠ECM
= ∠BCM. Значит, точки D, B, M и C лежат на одной окружности. Поэтому ∠MBC = ∠MDC = ∠DAC = ∠ACB. Значит, BM || AC, а так как треугольник ABC равнобедренный, то BM – биссектриса его внешнего угла при вершине B, то есть точка M лежит на прямой l, проходящей через точку B перпендикулярно биссектрисе данного угла.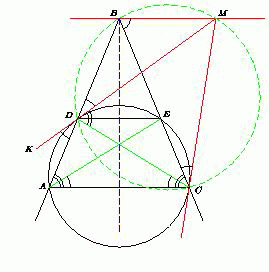 
Покажем теперь, что любая точка M прямой l, отличная от B, принадлежит искомому ГМТ. Для этого достаточно построить вспомогательную окружность, проходящую через точки B и M и пересекающую вторично каждую из сторон данного угла.
Ответ
Прямую, проходящую через B параллельно AC (без самой точки B).
Чтобы оставлять комментарии, войдите или зарегистрируйтесь