Олимпиадная задача по планиметрии для 8-9 класса: медианы и высоты треугольника
Задача
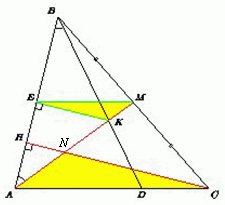
На стороне AC остроугольного треугольника ABC выбрана точка D. Медиана AM пересекает высоту CH и отрезок BD в точках N и K соответственно.
Докажите, что если AK = BK, то AN = 2KM.
Решение
Пусть E – проекция точки K на сторону AB. Тогда EM – средняя линия треугольника ABC. Значит, EM || AC и EM = ½ AC. Кроме того, EK || CH, поэтому треугольники EKM и CNA подобны по двум углам. Значит, AM : KM = AC : TM = 2 : 1.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет