Олимпиадная задача по планиметрии: четырёхугольник ABCD и условия для центра окружности

  Пусть точка O совпадает с точкой пересечения средних линий данного четырёхугольника. Обозначим через X и Y середины сторон AB и CD соответственно (рис. слева). Поскольку середины сторон любого четырёхугольника являются вершинами параллелограмма, а средние линии четырёхугольника – диагоналями этого параллелограмма, то O – середина XY.

  Предположим, что прямыеABиCDпересекаются в точкеP(пусть, для определённости, точкаPлежит на лучахABиDC). ПосколькуPO– биссектриса и медиана треугольникаXPY, то этот треугольник равнобедренный.   Обозначим  ∠XPY= 2α,  ∠BOX= β.  Тогда  ∠PXY= ∠PYX= 90° – α,  а так как  BOC– угол между биссектрисами внешних углов треугольникаBPC, то ∠BOC= 90° – α,  ∠COY= 180° – β – (90° – α) = 90° – β + α,  ∠OCY= 180° – (90° – β + α) – (90° – α) = β = ∠BOX.   Значит, треугольникиOXBиCYOподобны по двум углам. Следовательно,  OB:OC = XO:YO.  Аналогично  OA:OD = XA:YO = XB:YO = OB:OC,  откуда  OA·OC = OB·OD.   Пусть теперь  OA·OC = OB·OD  (рис. справа). Заметим, что

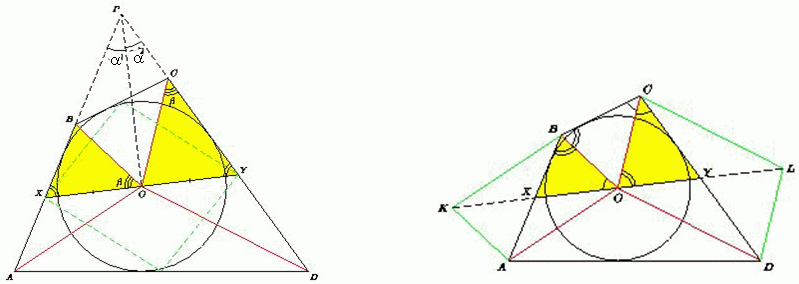
∠AOB + ∠COD = (180° – ∠OAB – OBA) + (180° – ∠OCD – ∠ODC) = 360° – ½ (∠DAB + ∠ABC + ∠BCD + ∠CDA) = 180°.

  Поэтому, если достроить треугольники OAB и OCD до параллелограммов AOBK и OCLD, то эти параллелограммы будут подобны (так как

OA : AK = OA : OB = DO : OC).  Поэтому треугольники OXB и CYO также будут подобны. Значит,  ∠XOB = ∠OCY = ∠OCB,  ∠COY = ∠XBO = ∠OBC.

  Следовательно,  ∠XOB + ∠BOC + ∠COY = ∠OCB + ∠BOC + ∠OBC = 180°,  то есть точка O лежит на прямой XY. Аналогично она лежит на прямой, соединяющей середины двух других сторон четырёхугольника, что и требовалось.

Ответ задачи отсутствует