Олимпиадная задача по планиметрии для 8–11 классов от Седракяна Н.

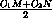Обозначим центры окружностей, описанных около треугольников ADB и ADC через O1и O2(рис.1), а середины отрезков BD , DC , MN , DO2и O1O2– через A1, A2, K , E и O соответственно. Пусть BAD = CAD = α . Тогда

BO1D = DO2C = 2α, A1O1D = A2O2D = α,

O1DO2 = 180^o - ( BDO1+ CDO2)=

=180^o - (90^o-α) -(90^o-α)= 2α.

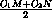Отрезок OK – средняя линия трапеции (или прямоугольника) O1MNO2, поэтому OK l и

OK = 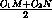= = 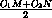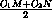+ 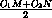= OE + EA2.

Заметим, что точки E , O и A2лежат на одной прямой, т.к.

OEO2 + O2EA2 = O1DO2 + O2EA2=

= O1DO2 + (180^o - DO2C)= 2α + (180^o-2α) = 180^o.

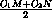Значит, OA2=OE + EA2=OK . Аналогично докажем, что OA1=OK . Поэтому точки A1, A2и K лежат на окружности с центром O , а т.к. OK l , то эта окружность касается прямой l .

Случай, когда вместо прямой l рассматривается прямая l1, разбирается аналогично.

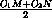Пусть радиусы окружностей 1и 2с центрами O1и O2, описанных около треугольников ADB и ADC , равны R1и R2соответственно. Если эти радиусы различны, то прямая l пересекает линию центров O1O2в некоторой точке Q (рис.2). Пусть QD пересекает эти окружности в точках B' и C' соответственно, а QA пересекает окружность 1в точке A' , отличной от A .

При гомотетии H с центром Q и коэффициентом k=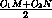 точки C' , D и A переходят в точки D , B' и A' соответственно, следовательно, DAC' = B'A'D . С другой стороны, B'A'D = B'AD , поэтому B'AD = C'AD . А это означает, что точки B' и C' совпадают с точками B и C , т.к. в противном случае один из углов BAD и CAD был бы меньше α , а другой – больше α ( α = B'AD = C'AD ).

Рассмотрим гомотетию H1с центром Q , переводящую 2в окружность, проходящую через точку E – середину отрезка MN . Из того, что l проходит через точку O икасается l следует, чтокасается l в точке E . Кроме того, из гомотетичности треугольников QNC и QMD (гомотетия H ) следует, что NC || MD . Кроме того H1(C) = C1, где EC1 || NC . Поэтому EC1– средняя линия трапеции CNMD , т.е. гомотетия H1переводит точку C в середину DC . Аналогично, она переводит D в середину отрезка BD . Значит,проходит через середины отрезков BD и DC .

Если же R1=R2, то вместо гомотетии следует рассмотреть параллельный перенос на вектор .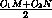

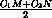
Ответ задачи отсутствует