Назад

Олимпиадная задача по планиметрии: треугольник ABC и касательная в точке Q, 8–9 класс, Емельянов Л. А.

Задача 208222 • Сложность: 3 • 8-9 класс
Задача

Дан треугольник ABC . На прямой AC отмечена точка B1так, что AB=AB1, при этом B1и C находятся по одну сторону от A . Через точки C , B1и основание биссектрисы угла A треугольника ABC проводится окружность, вторично пересекающая окружность, описанную около треугольника ABC , в точке Q . Докажите, что касательная, проведённая кв точке Q , параллельна AC .

Решение
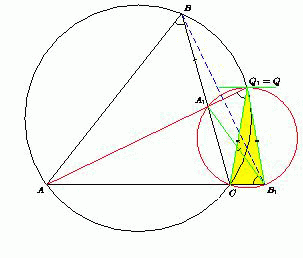
Пусть продолжение биссектрисы AA1треугольника ABC пересекает описанную окружность этого треугольника в точке Q1. Поскольку AB1 = AB , то точки B и B1симметричны относительно прямой AA1, поэтому

AB1A1 = ABA1 = ABC = AQ1C.

Значит, точки B1, C , A1и Q1лежат на одной окружности – описанной окружности треугольника A1B1C . Следовательно, точка Q1совпадает с точкой Q .

Тогда

QCB1 = QA1B1 = BA1Q = 180o - QMC = QB1C,

поэтому треугольник CQB1– равнобедренный. Следовательно, касательная, проведённая через вершину Q к его описанной окружности, параллельна основанию CB1. Что и требовалось доказать.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет