Олимпиадная задача о параллелограмме, окружностях и точке K (9

Задача

В параллелограмме ABCD на диагонали AC отмечена точка K . Окружность s1проходит через точку K и касается прямых AB и AD , причём вторая точка пересечения s1с диагональю AC лежит на отрезке AK . Окружность s2проходит через точку K и касается прямых CB и CD , причём вторая точка пересечения s2с диагональю AC лежит на отрезке KC . Докажите, что при всех положениях точки K на диагонали AC прямые, соединяющие центры окружностей s1и s2, будут параллельны между собой.

Решение

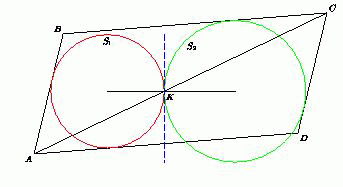
При гомотетии с центром K , переводящей вершину A в вершину C , луч AB переходит в противоположно направленный с ним луч CD , луч AD – в противоположно направленный с ним луч CB , окружность s1, вписанная вписанная в угол BAD , – в окружность s2, вписанную в угол DCB . Поскольку окружности s1и s2гомотетичны относительно их общей точки K , то они касаются в этой точке. Значит, у них есть общая касательная в точке K . Эта касательная перпендикулярна линии центров этих окружностей.

Пусть другой точке K' диагонали AC соответствует другая пара окружностей s1' и s2' . Окружности s1и s1' вписаны в угол BAD , следовательно, гомотетичны с центром в точке A , а значит, их касательные, проведённые в точках K и K' соответственно, параллельны. Тогда параллельны и перпендикулярные им линии центров пар окружностей s1, s2и s1' и s2' .

Ответ

Ответ задачи отсутствует

Олимпиадная задача по планиметрии с параллелограммом и окружностями для 9–11 классов

Задача

Решение

Ответ

Подтверждение удаления