Олимпиадная задача по планиметрии 8-9 класс — задача авторов Берлов и Кожевников

Задача

Окружность, вписанная в угол с вершиной O касается его сторон в точках A и B , K – произвольная точка на меньшей из двух дуг AB этой окружности. На прямой OB взята точка L такая, что прямые OA и KL параллельны. Пусть M – точка пересечения окружности, описанной около треугольника KLB , с прямой AK , отличная от K . Докажите, что прямая OM касается окружности.

Решение

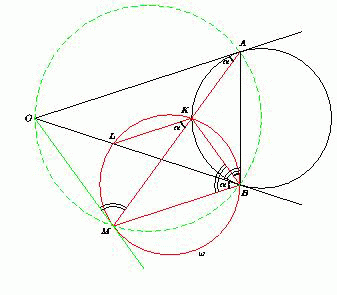
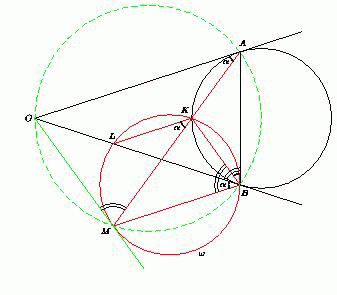Обозначим OAK = α . Поскольку OA || KL , то
LKM = OAK = α.

По теореме об угле между касательной и хордой

ABK = OAK = α.

Вписанные в окружностьуглы LKM и LBM опираются на одну и ту же дугу, поэтому

LBM = LKM = α.

Тогда из точек A и B , лежащих по одну сторону от прямой OM , отрезок OM виден под одним и тем же углом α . Значит, точки A , B , O и M лежат на одной окружности. Поэтому

OMK = OMA = OBA = OBK + ABK =

= OBK + α = OBK + OBM= KBM = LBM.

Тогда по теореме, обратной теореме об угле между касательной и хордой, OM – касательная к окружности.

Ответ

Ответ задачи отсутствует

Олимпиадная задача по планиметрии для 8-9 класса — доказательство касательности

Задача

Решение

Ответ

Подтверждение удаления