Олимпиадная задача по планиметрии и принципу Дирихле для 7-9 класса: внутрипятиугольника
Задача
Внутри выпуклого пятиугольника выбраны две точки. Докажите, что можно выбрать четырёхугольник с вершинами в вершинах пятиугольника так, что внутрь него попадут обе выбранные точки.
Решение
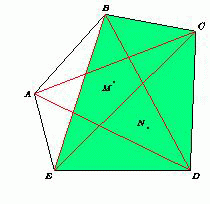
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет