Олимпиадная задача по планиметрии для 9-11 классов: доказательство о перпендикулярности прямых в треугольнике (Берлов С. Л.)
Задача
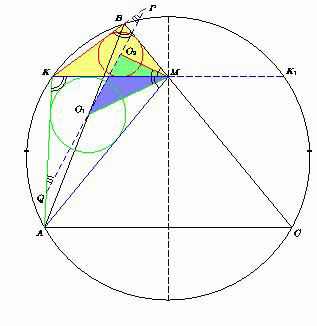
Серединный перпендикуляр к стороне AC треугольника ABC пересекает сторону BC в точке M. Биссектриса угла AMB пересекает описанную окружность треугольника ABC в точке K. Докажите, что прямая, проходящая через центры вписанных окружностей треугольников AKM и BKM, перпендикулярна биссектрисе угла AKB.
Решение
Поскольку MK – биссектриса внешнего угла при вершине M равнобедренного треугольника AMC, то MK || AC. Пусть продолжение отрезка MK за точку M пересекает описанную окружность треугольника ABC в точке K1. Дуги AK и CK1, заключённые между параллельными хордами KK1 и AC, равны. Поэтому ∠KBM = ∠KBC = ∠AKK1 = ∠AKM.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет