Олимпиадная задача по планиметрии: симметрия точек и площади в трапеции (Емельянов Л. А., 9-11 класс)

Заметим, что точки A' , B' , C' и D' определяются единственным образом.

Пусть AD – большее, а BC – меньшее основание трапеции ABCD , M – середина её средней линии PQ (точка P лежит на стороне AB ). Пусть прямые CM и AD пересекаются в точке C' (рис.1). Поскольку MQ – средняя линия треугольника CC'D , то C'D = 2MQ = PQ .

Значит, S_{Δ CC'D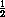} = S_ABCD . Таким образом, точка C' – одна из четырёх точек, о которых говорится в условии задачи. При этом, т.к. AD – большее основание трапеции, то AD>PQ = C'D , т.е. точка C' лежит на отрезке AD .

Проведя прямую BM , можно аналогично построить точку B' . Она также окажется на основании AD .

Пусть прямая, проведённая через точку C' параллельно диагонали AC , пересекает сторону CD в точке A' (рис.2). Рассмотрим трапецию ACA'C' . Пусть её диагонали пересекаются в точке T . Поскольку треугольники ATC' и CTA' равновелики, то равновелики и треугольники CC'D и AA'D , причём площадь каждого из двух последних треугольников равна половине площади трапеции. Аналогично строится четвёртая точка D' .

Диагонали AC и BD четырёхугольника ABCD соответственно параллельны диагоналям A'C' и B'D' четырёхугольника A'B'C'D' (рис.3), а т.к. середина M отрезка CC' равноудалена от прямых AC и A'C' (а также от прямых BD и B'D' ), то прямые A'C' и B'D' симметричны прямым AC и BD относительно середины M средней линии трапеции ABCD . Поскольку диагонали четырёхугольников ABCD и A'B'C'D' симметричны относительно точки M , то и точки их пересечения E и F симметричны относительно M .

Ответ задачи отсутствует