Назад

Олимпиадная задача по планиметрии для 7–9 классов от Лифшица Ю.: доказательство о треугольниках

Задача 208213 • Сложность: 3 • 7-9 класс
Задача

Дан треугольник ABC с попарно различными сторонами. На его сторонах построены внешним образом правильные треугольники ABC1, BCA1 и CAB1. Докажите, что треугольник A1B1C1 не может быть правильным.

Решение

  Предположим, что треугольник A1B1C1 – правильный.

  Если точка A лежит на отрезке B1C1, то из равенства  ∠C1B1A1 = ∠AB1C = 60°  следует, что C лежит на B1A1. При этом

∠BAC = 180° – ∠BAC1 – ∠CAB1 = 60°.  Аналогично,  ∠ACB = 60°.  Следовательно, треугольник ABC – правильный, что противоречит условию. Значит, точка A не лежит на B1C1.

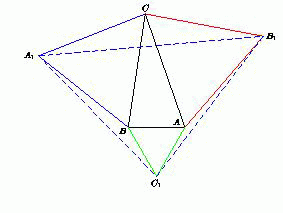
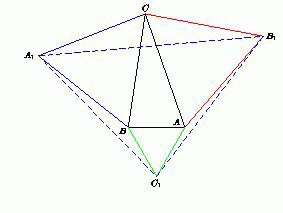
  Рассмотрим треугольники A1BC1, B1CA1 и C1AB1. Назовём один из них внешним, если он пересекается с треугольником ABC только по соответствующей вершине (так, на левом рисунке внешними являются треугольники A1BC1 и C1AB1, а на правом – треугольник A1BC1); иначе назовём его внутренним.

           
  Тогда к одной из вершин A1, B1, C1 прилегают либо два внешних треугольника (рис. слева), либо два внутренних (рис. справа). В первом случае соответствующий угол треугольника A1B1C1 больше 60°, во втором – меньше. Противоречие.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет