Олимпиадная задача по планиметрии: четырёхугольник ABCD, доказательство AF=BE
Задача
Дан четырёхугольник ABCD , в котором AB=AD и 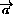 ABC=
ABC=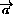 ADC=90o . На сторонах BC и CD выбраны соответственно точки F и E так, что DF
ADC=90o . На сторонах BC и CD выбраны соответственно точки F и E так, что DF 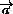 AE . Докажите, что AF
AE . Докажите, что AF 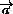 BE .
BE .
Решение
Обозначим 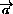 =
=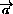 ,
, 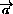 =
=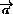
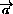 =
=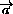 и
и 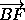 =
=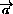 . Тогда
. Тогда
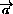 =
= 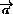 +
+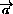 -
-
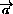 ,
,
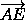 =
= 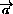 +
+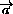 ,
,
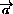 =
= 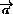 +
+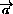 ,
,
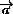 =
= 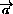 +
+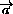 -
-
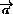 .
.
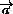 AE и AD
AE и AD 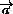 DE , поэтому
DE , поэтому
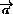 +
+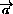 -
-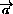 )(
)(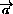 +
+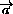 )=0.
)=0.
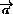 +
+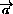 )(
)(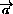 +
+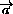 )
-
)
-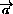 (
(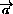 +
+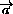 ) =
(
) =
(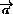 +
+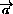 )(
)(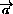 +
+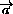 )-
|
)-
|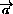 |2-
|2-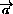 ·
· 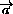 =
=
=(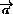 +
+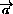 )(
)(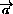 +
+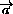 )-
|
)-
|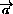 |2=0.
|2=0.
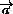 BF , а |
BF , а |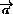 |=AB = AD= |
|=AB = AD= |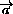 | ,
то
| ,
то
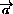 ·
· 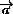 =
(
=
(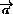 +
+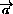 )(
)(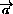 +
+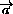 -
-
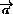 )=(
)=(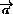 +
+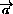 )(
)(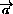 +
+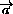 )-
|
)-
|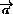 |2=
|2=
=(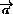 +
+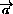 )(
)(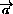 +
+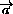 )-
|
)-
|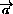 |2=0.
|2=0.
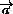 BE .
BE .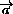
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет