Олимпиадная задача по планиметрии: Окружности и радиус описанной окружности
Задача
Две окружности радиусов R и r касаются прямой l в точках A и B и пересекаются в точках C и D . Докажите, что радиус окружности, описанной около треугольника ABC не зависит от длины отрезка AB .
Решение
Обозначим 
CAB= α , CBA = β .
Если ρ – радиус описанной окружности треугольника ABC , то по теореме синусов
AC=2R sin α =2ρ sin β, BC=2r sin β =2ρ sin α.
ρ2 sin α sin β = Rr sin α sin β.
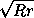, т.е. радиус описанной окружности
треугольника ABC зависит только от R и r .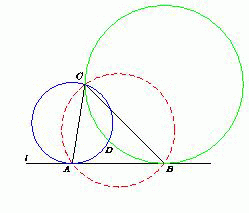
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет