Олимпиадная задача по планиметрии: медиана и биссектриса в треугольнике ABC, уровень 8-9 класс
Задача
В треугольнике ABC известно, что AA1– медиана, AA2– биссектриса, K – такая точка на AA1,
для которой KA2 || AC . Докажите, что AA2 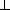 KC .
KC .
Решение
Обозначим векторы 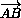 и
и 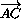 через
через 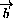 и
и 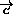 соответственно,
а их модули – через b и c .
Тогда
соответственно,
а их модули – через b и c .
Тогда
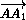 =
= 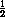 (
(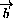 +
+
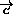 ).
).
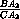 =
=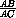 =
=  ,
,
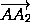 =
= 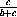
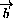 +
+
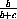
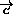 .
.
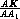 =
= 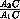 =
= 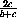
 AK=
AK=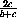 · AA1,
· AA1,
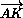 и
и 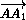 сонаправлены, то
сонаправлены, то
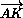 =
= 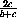
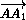 =
=
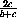 (
(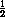 (
(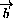 +
+
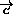 ))=
))=
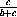
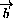 +
+ 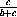
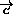 .
.
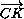 =
= 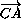 +
+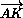 =
-
=
-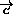 +
+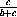
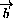 +
+
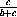
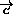 =
=
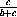
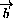 -
-
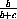
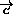 .
.
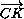 ·
· 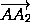 =
(
=
(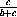
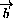 +
+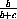
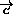 )(
)(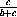
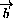 -
- 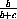
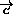 )=
)=
=(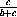 )2· b2 - (
)2· b2 - (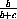 )2· c2
=0.
)2· c2
=0.
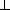 KC .
KC .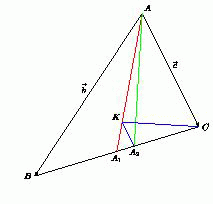
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет