Олимпиадная задача по планиметрии для 8–9 класса: центр вписанной и описанной окружностей в равнобедренном треугольнике
Задача
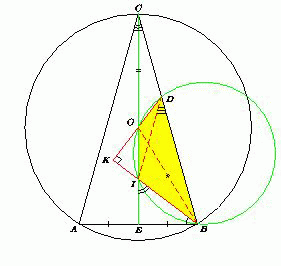
В равнобедренном треугольнике ABC (AC = BC) точка O – центр описанной окружности, точка I – центр вписанной окружности, а точка D на стороне BC такова, что прямые OD и BI перпендикулярны. Докажите, что прямые ID и AC параллельны.
Решение
Если данный треугольник равносторонний (точки O и I совпадают), то утверждение очевидно.
Проведём высоту CE. Пусть точка O лежит между точками I и C (∠B > 60°), а прямые OD и BI пересекаются в точке K. Положим ∠B = ∠A = 2α. Тогда ∠EBI = ∠DBI = α, BIE = 90° – α = ∠BDK, ∠BIO = 180° – ∠BIE = 90° + α.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет