Олимпиадная задача по планиметрии: пересечение прямых в треугольнике (Сонкин М.)
Задача
Дан треугольник ABC. Точка B1 делит пополам длину ломаной ABC (составленной из отрезков AB и BC), точка C1 делит пополам длину ломаной ACB, точка A1 делит пополам длину ломаной CAB. Через точки A1, B1 и C1 проводятся прямые lA, lB и lC, параллельные биссектрисам углов BAC, ABC и ACB соответственно. Докажите, что прямые lA, lB и lC пересекаются в одной точке.
Решение
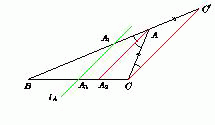
Пусть для определённости AB ≥ AC. На продолжении стороны AB за точку A отложим отрезок AC' равный AB. Тогда треугольник CAC' – равнобедренный и ∠AC'C = ½ ∠BAC. Значит, прямая CC' параллельна биссектрисе AA2 треугольника ABC. Поскольку прямая lA проходит через середину A1 стороны BC' треугольника BCC' и параллельна CC', то она проходит через середину A3 стороны BC. Аналогично прямые lB и lC проходят через середины B3 и C3 сторон AC и AB. При гомотетии с центром в точке пересечения медиан треугольника ABC и коэффициентом –½ треугольник ABC переходит в треугольник A3B3C3, а прямые, содержащие биссектрисы углов A, B и C, – в прямые lA, lB и lC соответственно. Следовательно, прямые lA, lB и lC пересекаются в одной точке.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь