Олимпиадная задача по планиметрии и комбинаторной геометрии для 7-9 классов: покрытие треугольника квадратами
Задача
Докажите, что остроугольный треугольник полностью покрывается тремя квадратами, построенными на его сторонах как на диагоналях.
Решение
Пусть KC – квадрат, построенный на стороне AB треугольника ABC как на диагонали. Аналогично определяются квадраты KA и KB .
Пусть O – точка пересечения биссектрис треугольника ABC .
Поскольку 
BAC < 90o и ABC < 90o ,
то BAO < 45o и ABO < 45o .
Значит, все точки треугольника AOB лежат внутри квадрата KC ,
т.е. треугольник AOB покрывается квадратом KC .
Аналогично, треугольники BOC и AOC покрываются квадратами KA и KB соответственно.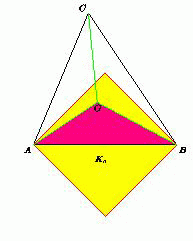
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет