Олимпиадная задача по планиметрии: угол между прямыми DM и KE в треугольнике
Задача
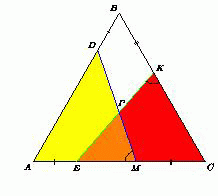
На сторонах AB и BC равностороннего треугольника ABC взяты точки D и K, а на стороне AC – точки E и M, причём DA + AE = KC + CM = AB.
Докажите, что угол между прямыми DM и KE равен 60°.
Решение
Пусть прямые DM и KE пересекаются в точке P. Из условия следует, что CE = AC – AE = AD. Аналогично, CK = AM. Поэтому треугольники MAD и ECK равны по двум сторонам и углу между ними. Значит, ∠MPE = 180° – ∠PME – ∠PEM = 180° – ∠PKC – ∠PEC = ∠C = 60°.
Если отрезки DM и EK не пересекаются, то аналогичные рассуждения проводятся для вертикальных углов.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет