Назад

Олимпиадная задача по планиметрии: биссектриса в прямоугольном треугольнике, 8-9 класс

Задача 208166 • Сложность: 3 • 8-9 класс
Задача

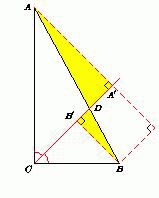
Докажите, что в прямоугольном треугольнике биссектриса, проведённая из вершины прямого угла, не превосходит половины проекции гипотенузы на прямую, перпендикулярную этой биссектрисе.

Решение

  Пусть CD – биссектриса, проведённая из вершины прямого угла C прямоугольного треугольника ABC,  A' и B' – проекции вершин A и B на прямую CD (см. рис.). Будем считать, что  AC ≥ BC.  По свойству биссектрисы  AD/DB = AC/BC ≥ 1.

  Прямоугольные треугольникиADA'иBDB'подобны, поэтому  A'D/DB' = AD/DB≥ 1  ⇒  A'D ≥ B'D  ⇒  CD≤ ½ (CB' + CA').   Поскольку  ∠ACA'= ∠BCB'= 45°,  то  CA' = AA'  и  CB' = BB'.  Следовательно,  CD≤ (CB' + CA') = ½ (AA' + BB').  Но  AA' + BB'  и есть длина проекции гипотенузы на любую прямую, перпендикулярную биссектрисеCD.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет