Олимпиадная задача по планиметрии для 8-9 класса от Произволова В. В.
Задача
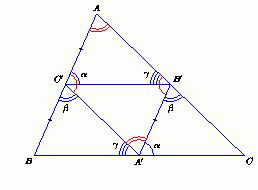
В треугольнике ABC точки A', B', C' лежат на сторонах BC, CA и AB соответственно. Известно, что ∠AC'B' = ∠B'A'C, ∠CB'A' = ∠A'C'B, ∠BA'C' = ∠C'B'A. Докажите, что точки A', B', C' – середины сторон треугольника ABC.
Решение
Углы AC'A' и AB'A' равны, так как дополняют до 180° равные углы CB'A' и A'C'B. Углы B'AC' и B'A'C' равны, так как дополняют до 180° равные суммы ∠C'B'A + ∠AC'B' и ∠BA'C' + ∠B'A'C. Значит, AB'A'C' – параллелограмм. Следовательно, AC' = B'A'. Аналогично C'B = B'A'. Поэтому AC' = C'B, то есть C' – середина AB. Для точек B' и A' доказательство аналогично.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет