Олимпиадная задача по планиметрии «Параллелограмм и точка M» (8-9 класс, Смуров М. В.)
Задача
На стороне AB параллелограмма ABCD (или на её продолжении) взята точка M, для которой ∠MAD = ∠AMO, где O – точка пересечения диагоналей параллелограмма. Докажите, что MD = MC.
Решение
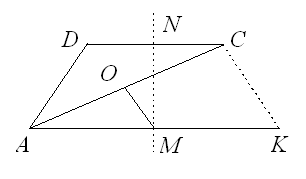
Пусть K – точка, симметричная точке A относительно перпендикуляра MN к прямой AB (см. рис.). Тогда AM = MK и, следовательно, MO – средняя линия треугольника CAK. Поэтому CK || MO и ∠MKC = ∠AMO = ∠MAD. Значит, при симметрии относительно MN прямая AD переходит в прямую KC. Точка, симметричная точке D относительно MN, находится, с одной стороны, на перпендикуляре DC к MN, а с другой – на образе KC прямой AD при этой симметрии, то есть совпадает с C. Таким образом, отрезки MD и MC симметричны относительно MN и потому равны.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь