Назад

Олимпиадная задача по планиметрии для 9–11 классов с четырёхугольником и окружностями

Задача 208149 • Сложность: 4 • 9-11 класс
Задача

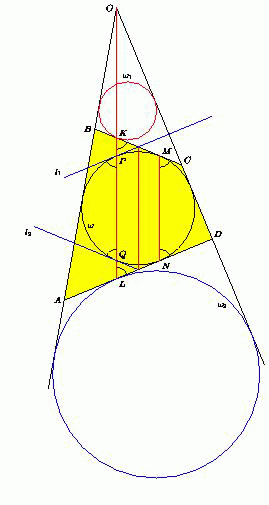
Четырёхугольник ABCD описан около окружности ω. Продолжения сторон AB и CD пересекаются в точке O. Окружность ω1 касается стороны BC в точке K и продолжений сторон AB и CD; окружность ω2 касается стороны AD в точке L и продолжений сторон AB и CD. Известно, что точки O, K и L лежат на одной прямой. Докажите, что середины сторон BC, AD и центр окружности ω лежат на одной прямой.

Решение

  Пусть для определённости точка O лежит на продолжении отрезка AB за точку B. Обозначим через P и Q точки пересечения KL с окружностью ω, через M и N – точки касания сторон BC и AD с ω. Проведём касательные l1 и l2 к ω в точках P и Q. Обозначим через α угол между касательной l1 (или l2) и хордой PQ.

  При гомотетии с центромO, переводящей окружность ω1в окружность ω, касательнаяBCв точкеKперейдёт вl2; при гомотетии с центромO, переводящей окружность ω2в ω, прямаяADперейдёт вl1. Поэтому  BC || l2,  AD || l1и, следовательно,  ∠LKC= α = ∠KLD.   Кроме того,  ∠BMN= ∠ANM  как углы между касательной и хордой. Отсюда следует, что четырёхугольникKLNM– равнобедренная трапеция и ∠NMC= ∠MND= α.  Таким образом, хордыPQиMNпараллельны и стягивают равные дуги величины 2α. Следовательно, средняя линия этой трапеции проходит через центр окружности ω. Но серединаKMсовпадает с серединойBC(см. задачу155404), и серединаLNсовпадает с серединойAD.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет