Олимпиадная задача по планиметрии: параллелограмм BPB₁Q, 9–11 класс, Емельянов Л. А.

Пусть точки Q и B1лежат по разные стороны от прямой BK , а точки P и B1– по разные стороны от прямой BM (остальные случаи рассматриваются аналогично). Поскольку при гомотетии с центром в точке N , переводящей внутреннюю окружность во внешнюю, касательная BC к внутренней окружности переходит в параллельную BC касательную B'C' к внешней окружности, то точка касания B'C' с внешней окружностью есть середина дуги BC внешней окружности, не содержащей точку N , т.е. точка P . Значит, точки N , M и P лежат на одной прямой. Аналогично докажем, что точки N , K и Q также лежат на одной прямой.

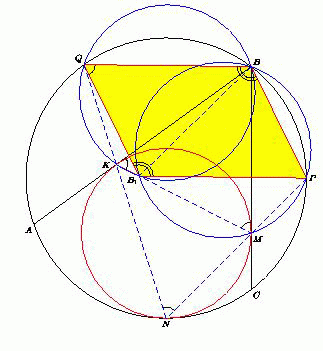
Четырёхугольники BPNQ , BQKB1и BPMB1– вписанные, поэтому

BQN + BPN = 180^o, BQK + BB1K = 180^o, BPM + BB1M = 180^o.

Тогда

BB1K+ BB1M = (180^o- BQK) +(180^o- BPM)=

=360^o - ( BQK+ BPM) =360^o - ( BQN+ BPN)= 360^o-180^o=180^o,

т.е. точка B1лежит на отрезке KM .

Поскольку BK и BM – касательные, проведённые из точки B к внутренней окружности, то треугольник BKM – равнобедренный, поэтому BKM= BMK . Тогда из теоремы о вписанных углах, опирающихся на одну и ту же дугу, и из теоремы об угле между касательной и хордой следует, что

BQB1 = BKB1= KNM = BMK = BMB1= BPB1,

PB1Q = PB1B+ QB1B = PMB + QKB = CMN + AKN =

= MKN + KMN = 180^o- MNK = 180^o- PNQ = PBQ.

Значит, противоположные углы четырёхугольника BPB1Q попарно равны. Следовательно, BPB1Q – параллелограмм.

Ответ задачи отсутствует