Назад

Олимпиадная задача по планиметрии: точки на окружности в треугольнике ABC, 8–9 класс

Задача 208147 • Сложность: 3 • 8-9 класс
Задача

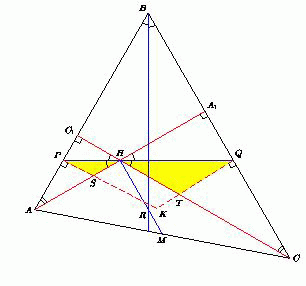
В остроугольном неравнобедренном треугольнике ABC биссектриса угла между высотами AA1 и CC1 пересекает стороны AB и BC в точках P и Q соответственно. Биссектриса угла B пересекает отрезок, соединяющий ортоцентр H треугольника ABC с серединой M стороны AC в точке R. Докажите, что точки P, B, Q и R лежат на одной окружности.

Решение

  Пусть перпендикуляр, восставленный к сторонеABв точкеP, пересекает высотуAA1в точкеS, а перпендикуляр, восставленный к сторонеBCв точкеQ, пересекает высотуCC1в точкеT. ЕслиK– точка пересечения этих перпендикуляров, то точкиPиQлежат на окружности с диаметромBK. Утверждение задачи равносильно тому, что точкаKсовпадает сR(см. рис.).

  Поскольку  ∠BPQ= ∠C1PH= 90° – ∠C1HP= 90° – ∠CHQ= 90° – ∠AHQ= ∠A1QH= ∠BQP,  то треугольникPQB– равнобедренный:  BP = BQ.  Из равенства прямоугольных треугольниковBPKиBQKследует, что точкаKлежит на биссектрисе углаB. Осталось доказать, что точкаKлежит на прямойHM.   Действительно, треугольникPHC1подобен треугольникуQHA1, треугольникAHC1– треугольникуCHA1, а треугольникPHS– треугольникуTHQ, поэтому  HS:HT = PH:HQ = CH1:HA1=AH:HC.   Значит,  ST || AC.  Поэтому медианаHMтреугольникаAHCпроходит через серединуOотрезкаST, а так какO– точка пересечения диагоналей параллелограммаHTKS, то точкаKлежит на прямойHO, а значит, на прямойHM.   Следовательно,K– точка пересечения прямойMHс биссектрисой углаB, а значит, совпадает с точкойR.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет