Назад

Олимпиадная задача по планиметрии для 8-9 класса от Сонкина М.: Симметрия на окружностях

Задача 208145 • Сложность: 3 • 8-9 класс
Задача

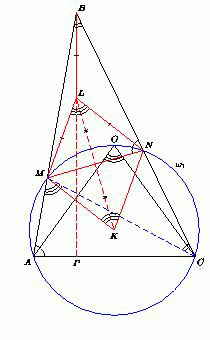
Пусть O – центр описанной окружности ω остроугольного треугольника ABC. Окружность ω1 с центром K проходит через точки A, O и C и пересекает стороны AB и BC в точках M и N. Известно, что точки L и K симметричны относительно прямой MN. Докажите, что  BL ⊥ AC.

Решение

  Пусть  ∠A = α,  ∠B = β.  Поскольку AOC – центральный угол окружности ω, а угол ABC – вписанный, то  ∠AOC = 2β.

  Вписанные в окружность ω1 углы AMC и AOC равны.

  Поскольку AMC – внешний угол треугольника BMC, то   BCM = ∠AMC – ∠MBC = 2β – β = β,  а так как MKN – центральный угол окружности ω1, то

∠MKN = 2∠MCN = 2∠MCB = 2β.

  ЧетырёхугольникAMNCвписан в окружность ω1, поэтому  ∠BNM= α.   Поскольку точкаLсимметрична точкеKотносительно прямойMN, то  ∠MLN= ∠MKN= 2β,  а так как  LM = MK = KN = LN  и  ∠MBN= ½ ∠MLN,  тоL– центр описанной окружности треугольникаMBN. Центральный уголBLMэтой окружности вдвое больше вписанного углаBNM, то есть равен 2α. Из равнобедренного треугольникаBLMнаходим, что  ∠MBL= 90° – α.   Пусть прямыеBLиACпересекаются в точкеP. Тогда  ∠APB= 180° – ∠ABP– ∠BAP= 180° – (90° – α) – α = 90°.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет