Олимпиадная задача по планиметрии: биссектриса в параллелограмме (8–9 класс)
Задача
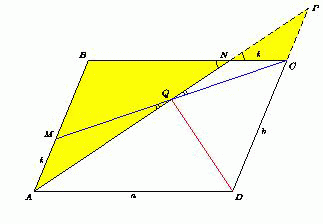
В параллелограмме ABCD на сторонах AB и BC выбраны точки M и N соответственно, причём AM = CN, Q – точка пересечения отрезков AN и CM.
Докажите, что DQ – биссектриса угла D.
Решение
Пусть прямые AN и CD пересекаются в точке P. Из подобия треугольников PNC и ANB следует, что PQ : AQ = PC : AM = PC : CN.
Из подобия треугольников PNC и PAD имеем PC : CN = PD : AD.
Поэтому PD : AD = PQ : AQ, то есть DQ – биссектриса треугольника ADP.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет