Олимпиадная задача по планиметрии: центр описанной окружности и точки пересечения
Задача
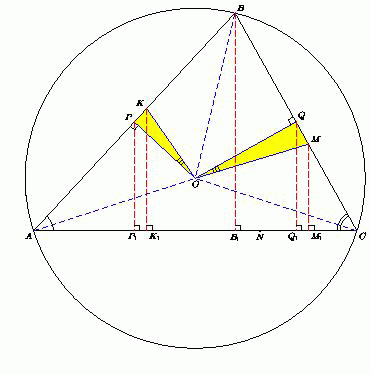
На большей стороне AC треугольника ABC взята точка N так, что серединные перпендикуляры к отрезкам AN и NC пересекают стороны AB и BC в точках K и M соответственно. Докажите, что центр O описанной окружности треугольника ABC лежит на описанной окружности треугольника KBM.
Решение
Пусть P и Q – середины сторон AB и BC соответственно, P1, K1, Q1, M1, B1 – проекции точек P, K, Q, M, B на сторону AC. Поскольку P1 – середина AB1, а Q1 – середина CB1, то P1Q1 = ½ AB1 + ½ CB1 = ½ AC.
Поскольку K1 – середина AN, а M1 – середина CN, то K1M1 = ½ AN + ½ CN = ½ AC = P1Q1.
Поэтому, если точка K ближе к вершине B, чем точка P, то точка Q ближе к B, чем точка M. Поскольку OP ⊥ AB и OQ ⊥ BC, то ∠POQ = 180° – ∠B.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь