Олимпиадная задача по планиметрии: равенство углов внутри параллелограмма (8-9 класс)
Задача
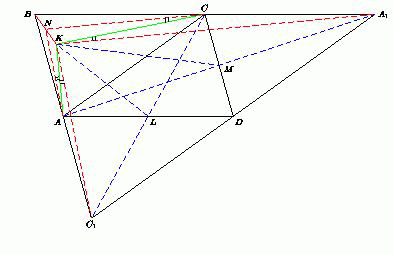
Внутри параллелограмма ABCD выбрана точка K так, что середина стороны AD равноудалена от точек K и C, а середина стороны CD равноудалена от точек K и A. Точка N – середина отрезка BK. Докажите, что углы NAK и NCK равны.
Решение
Пусть M – середина CD, а L – середина AD. Достроим параллелограмм ABCD до треугольника BA1C1 так, чтобы отрезок AC был средней линией этого треугольника. ACA1D и CAC1D – параллелограммы, а точки A, M и A1 лежат на одной прямой. В треугольнике AKA1 медиана KM равна половине AM стороны AA1, значит, ∠AKA1 = 90°. Аналогично ∠CKC1 = 90°. Таким образом, ∠CKA1 = 90° – ∠A1KC1.
Источники и прецеденты использования
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет