Назад

Геометрическое место вершин прямоугольника: олимпиадная задача по планиметрии

Задача 208132 • Сложность: 3 • 8-9 класс
Задача

Дана окружность и точка A внутри неё.

Найдите геометрическое место вершин C всевозможных прямоугольников ABCD, где точки B и D лежат на окружности.

Решение

  Пусть O центр данной окружности, R – её радиус. Обозначим,  OA = a.  Поскольку  OB = OD = R  и  OA² + OC² = OB² + OD²  (см. задачу 154405),  то

OC² = OB² + OD² – OA² = 2R² – a².

  Значит, точка C лежит на окружности (обозначим её Ω) с центром O и радиусом   .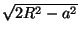

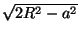
  Обратно, пустьC'– произвольная точка окружности Ω. На отрезкеAC'как на диаметре построим окружность. Она пересекает данную окружность в двух точках. ПустьB– любая из них. Рассмотрим прямоугольникABCD, о котором говорится в условии задачи, лежащий по ту же сторону отAB, что и точкаC'. По ранее доказанному точкаCлежит на окружности Ω, а так как  CB⊥AB  и  C'B⊥AB,  то точкиCиC'совпадают.
Ответ

Окружность с центром О и радиусом 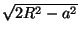   (R – радиус, О – центр данной окружности,  a = OA).

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет