Олимпиадная задача по планиметрии для 8-9 классов: вписанный четырёхугольник
Задача
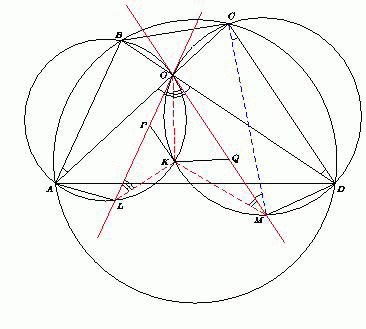
Диагонали вписанного четырёхугольника ABCD пересекаются в точке O. Пусть описанные окружности S1 и S2 треугольников ABO и CDO второй раз пересекаются в точке K. Прямые, проходящие через точку O параллельно прямым AB и CD, вторично пересекают S1 и S2 в точках L и M соответственно. На отрезках OL и OM выбраны соответственно точки P и Q, причём OP : PL = MQ : QO. Докажите, что точки O, K, P, Q лежат на одной окружности.
Решение
Не умаляя общности, можно считать, что ∠ABO ≥ ∠BAO, тогдаABOLиDCOM– равнобедренные трапеции. Из теоремы о вписанных углах следует, что ∠LOA= ∠OAB= ∠ODC= ∠DOM= ∠DCM= ∠CMO, а так как ∠KMC= 180° – ∠KOC= ∠KOA, то ∠KMO= ∠KOL. Аналогично ∠KLO= ∠KOM. Значит, треугольникиKOMиKLOподобны по двум углам. Но тогда подобны и треугольникиKOPиKMQ (OP:PL = MQ:QO по условию). Поэтому ∠KPO= ∠KQM, и четырёхугольникKPOQ– вписанный.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь