Олимпиадная задача по планиметрии: параллельность отрезков в пересекающихся окружностях для 8-9 классов
Задача
Окружности S1 и S2 с центрам O1 и O2 соответственно пересекаются в точках A и B. Касательные к S1 и S2 в точке A пересекают отрезки BO2 и BO1 в точках K и L соответственно. Докажите, что KL || O1O2.
Решение
Обозначим ∠BAL = α, BAK = β. Тогда ∠AO2B = 2∠BAL = 2α, ∠AO1B = 2BAK = 2β, поэтому ∠BO2O1 = ½ AO2B = α, ∠BO1O2 = ½ ∠AO1B = β.
Из треугольника O1BO2 находим, что ∠O1BO2 = 180° – α – β = 180° – ∠LAK.
Значит, четырёхугольник AKBL – вписанный. Тогда ∠KLB = ∠KAB = β = ∠O2O1B. Следовательно, KL || O1O2. 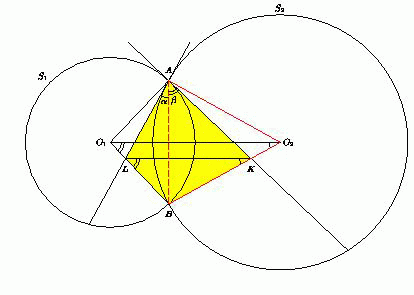
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет