Олимпиадная задача Шестакова С. А. по планиметрии для 8–9 класса: площади треугольников в четырёхугольнике
Задача
В выпуклом четырёхугольнике ABCD точки E и F являются серединами сторон BC и CD соответственно. Отрезки AE, AF и EF делят четырёхугольник на четыре треугольника, площади которых равны (в каком-то порядке) последовательным натуральным числам. Каково наибольшее возможное значение площади треугольника ABD?
Решение
Пусть площади треугольников равны n, n + 1, n + 2 и n + 3. Тогда SABCD = 4n + 6. EF – средняя
линия треугольника BCD, поэтому SBCD = 4SECF ≥ 4n. Следовательно, SABD = SABCD – SBCD ≤ 6.
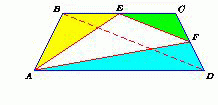
Покажем, что эта площадь может равняться 6. Рассмотрим равнобедренную трапецию ABCD с основаниями AD = 6, BC = 4 и высотой 2. Тогда
SCFЕ = 1, SABE = 2, SADF = 3, SAEF = SABCD – 1 – 2 – 3 = 4, и при этом SABD = 6.

Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет