Олимпиадная задача по планиметрии для 7-9 классов: перпендикулярность прямых в пересекающихся окружностях
Задача
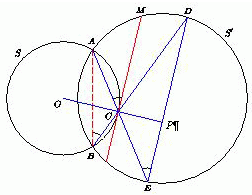
Окружность S с центром O и окружность S' пересекаются в точках A и B. На дуге окружности S, лежащей внутри S', взята точка C. Точки пересечения прямых AC и BC с S', отличные от A и B, обозначим через E и D соответственно. Докажите, что прямые DE и OC перпендикулярны.
Решение
Решение 1: Пусть касательная к окружности S, проведённая через точку C, пересекает окружность S' в точке M, лежащей на дуге AD, не содержащей точки E. Тогда
∠ACM = ∠ABC = ∠AED.
Поэтому CM || DE, а так как OC ⊥ CM как радиус, проведённый в точку касания, то OC ⊥ DE.
Решение 2: Пусть α = ∠BDE = ∠BAE = ∠BAC.
Из равнобедренного треугольника BOC находим, что ∠ BCO = ½ (180° – ∠BOC) = ½ (180° – 2α) = 90° – α.
Пусть P – точка пересечения прямых DE и OC. Тогда ∠DCP = ∠BCO = 90° – α.
Следовательно, ∠CPD = 180° – (∠DCP + ∠CDP) = 180° – (∠DCP + ∠BDE) = 180° – (90° – α + α) = 90°, то есть DE ⊥ OC.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь