Олимпиадная задача по планиметрии: угол между хордами в пересекающихся окружностях для 8–9 класса
Задача
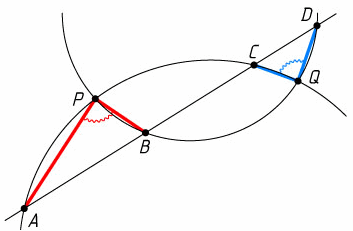
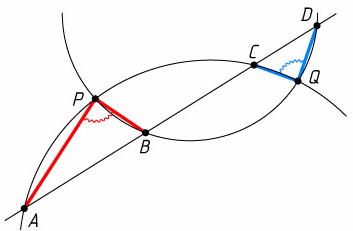
Две окружности пересекаются в точках P и Q. Прямая пересекает эти окружности последовательно в точках A, B, C и D, как показано на рисунке.
Решение
По теореме о вписанных углах ∠PAC = ∠PQC, ∠PBD = ∠PQD.
Поскольку PBD – внешний угол треугольника ABP, то ∠PBD = ∠PAB + ∠APB.
Следовательно, ∠APB = ∠PBD – ∠PAB = ∠PBD – PAC = ∠ PQD – ∠PQC = ∠CQD.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет